Die Sudoku Strategie „naked Subsets“ (nackte Teilmengen) reduziert Kandidaten aus den ermittelten Kandidatenlisten, so dass weitere Einer hervortreten.
Kapitel überspringen und gleich zur Sudoku-Spielplattform.
Inhalt Teil 7
Im Teil 6: Sudoku hidden Subsets wurde bereits eine Teilmengen-Methode vorgestellt, Kandidatenlisten zu reduzieren. Die Sudoku Strategie „naked Subsets“ oder „nackte Teilmengen“ beruht ebenfalls auf Kombinationen in den Kandidatenlisten mehrerer Feldern einer Zeile, Spalte oder eines Blocks. Dabei werden jedoch Kandidaten aus den anderen Feldern der Zeile, Spalte oder des Blocks eliminiert.
Naked Subsets (nackte Teilmengen)
Unter dem Begriff naked Subset (nS) versteht man Kandidaten-Kombinationen, die jeweils gemeinsam in der gleichen Zeile, Spalte oder Block vorkommen, und die einzigen Kandidaten dieser Felder (also „nackt“) sind. Stehen die Kandidaten-Kombinationen in der gleichen Zeile, Spalte oder dem gleichen Block, können diese Kandidaten aus allen anderen Feldern dieser Zeile, Spalte oder des Block eliminiert werden. Bei den Kandidaten-Kombinationen kann es sich um zwei Zahlen (Paare), drei Zahlen (Tripel) usw. handeln. Man muss sie dann entsprechend in zwei, drei usw. Feldern finden.
Beispiel/ naked Subset
Betrachten wir dazu Zeile 1 in den oberen drei Blöcken 1, 2 und 3 des sehr schwierigen Sudokus „sudoku_4_sehr_schwierig.txt“. In zwei Feldern dieser Zeile findet man die Ziffernfolge 13 in der Kandidatenliste. Die Ziffern 13 treten dabei als Paar und ohne weitere Kandidaten (also „nackt“) in der Kandidatenliste dieser beiden Felder auf. Ein naked Subset (nS) (nackte Teilmenge) ist gefunden.
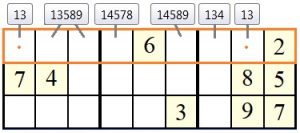
Dies bedeutet, dass eine der beiden Ziffern 13 im linken Feld, und die andere Ziffer im rechten Feld stehen muss. Für alle anderen Felder der Zeile fallen demnach die Kandidaten 1 und 3 weg und können aus den Kandidatenlisten dieser Felder eliminiert werden. Nach der Bereinigung lässt sich in Block 3 direkt ein nackter Einer finden, die 4:
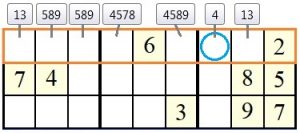
Sudoku-Spielplattform/ naked Subset
Spielt man das sehr schwierige Sudoku „sudoku_4_sehr_schwierig.txt“ mit der Strategie der naked Subsets (nS) (nackten Teilmenge) auf der Sudoku-Spielplattform nach, ergibt sich u. a. folgendes:
Spielzug 1
…
Zeile 1 – nS (13) || Z1 #2 (#2): 13589=>589
Zeile 1 – nS (13) || Z1 #3 (#3): 13589=>589
Zeile 1 – nS (13) || Z1 #4 (#4): 14578=>4578
Zeile 1 – nS (13) || Z1 #6 (#6): 14589=>4589
Zeile 1 – nS (13) || Z1 #7 (#7): 134=>4
=> Zeile 1 beherbergt einen naked Subset (nS) (nackte Teilmenge), nämlich das Ziffernpaar 13. Von der Bereinigung betroffen sind in Zeile 1 die Felder #2, #3, #4, #6 und #7. Die Kandidatenlisten dieser Felder werden bereinigt, d. h. es werden die Ziffern 1 und 3 aus deren Kandidatenlisten eliminiert.
Daraus ergibt sich direkt:
Zeile 1/ Spalte 7/ B3 #1 (#7): – nE
=> In Zeile 1, Spalte 7, Block 3, Feld #1 dieses Blocks (Feld #7) findet sich mit der Ziffer 4 ein nackter Einer.
Weitere Beispiele
Beim weiteren Spiel wird man feststellen, dass man weitere Strategien für dieses sehr schwierige Sudoku benötigt. Kombiniert man von Anfang an die Strategie der lokalen linearen Suche (lS), der hidden Subsets (hS) und der naked Subsets (nS), benötigt man für das sehr schwierige Sudoku „sudoku_4_sehr_schwierig.txt“ auf der Sudoku-Spielplattform neun Spielzüge.
Mit den gleichen Einstellungen benötigt man für das 17er-Sudoku „sudoku_17er.txt“ auf der Sudoku-Spielplattform elf Spielzüge .
Am Ende von Teil 7
Mit den bisherigen drei Sudoku-Strategien Kandidatenlisten zu reduzieren, knackst du inzwischen sehr schwierige sowie auch einige ultimativ schwierige Sudokus. Natürlich aber noch längst nicht alle! Hierfür gilt es weitere Strategien zu erlernen – einige davon sind in den folgenden Kapiteln gezeigt.
Zum nächsten Kapitel Teil 8: Sudoku X-Wing.
Mit einem Klick finanziert