Die Sudoku Strategie „hidden Subsets“ (versteckte Teilmengen) reduziert Kandidaten aus Feldern ermittelter Kandidatenlisten, so dass weitere Einer hervortreten.
Kapitel überspringen und gleich zur Sudoku-Spielplattform.
Inhalt Teil 6
Im Teil 5: Sudoku lineare lokale Suche wurde bereits eine Methode vorgestellt, Kandidatenlisten zu reduzieren. Die Sudoku Strategie „hidden Subsets“ oder „versteckte Teilmengen“ stellt eine weitere Methode dar, die auf Teilmengen (Paare, Tripel etc.) in den Kandidatenlisten einer Zeile, Spalte oder eines Blocks beruht. Findet man solche Teilmengen innerhalb der Kandidaten einer Zeile, Spalte oder eines Blocks, lassen sich alle restlichen Kandidaten aus diesen Feldern eliminieren.
Hidden Subsets (versteckte Teilmengen)
Unter einem hidden Subset versteht man im einfachsten Fall zwei Ziffern, die als Paar gemeinsam in derselben Zeile, Spalte oder Block, aber eben genau nur zweimal, bzw. in nur zwei gemeinsamen Feldern vorkommen, unabhängig von den weiteren Kandidaten, die diese Felder aufweisen. Da unter den Kandidaten neben diesem Ziffernpaar auch andere Kandidaten vorkommen können, handelt es sich bei dem Ziffernpaar jeweils um eine versteckte Teilmenge der Kandidaten dieser Felder. Ist dies der Fall, bedeutet das, dass diese Felder für genau dieses Ziffernpaar reserviert sind, auch wenn man noch nicht weiß, welche Ziffer an welcher Stelle der Zeile, Spalte oder des Blocks stehen wird. Daher können alle anderen Kandidaten aus diesen Feldern eliminiert werden, so dass nur noch die versteckte Teilmenge als Kandidaten stehen bleiben.
Hidden Subsets gibt es nicht nur in Form von Zweier-Paaren, auch Tripel oder noch höhere Ziffernzahlen als versteckte Teilmenge sind möglich. Entsprechend müssen diese dann in genau zwei, drei oder entsprechend vielen Feldern derselben Zeile, Spalte oder desselben Blocks auftreten.
Beispiel/ hidden Subset
Betrachten wir dazu Block 8 der unteren drei Blöcken 7, 8 und 9 des 21er-Sudoku „sudoku_21er.txt“. In der oberen Zeile können die Ziffern 2 und 6 nicht mehr vorkommen, da diese Zeile bereits durch diese zwei Zahlen aus den benachbarten Blöcken gesperrt ist. In der mittleren Zeile von Block 8 sind bereits alle Felder durch Zahlen belegt. Bleibt die untere Zeile, in der die Ziffern 2 und 6 nur noch in zwei von drei freien Felder vorkommen können:
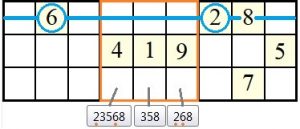
Die Ziffern 2 und 6 treten als Paar und als Teilmenge (unter anderen Kandidaten in) der Kandidatenliste dieser beiden Felder auf. Ein hidden Subset (versteckte Teilmenge) ist gefunden.
Die Kandidatenliste der beiden Felder kann daher auf die beiden Ziffern 26 bereinigt werden, denn in einem der beiden Felder wird die 2, im anderen die 6 stehen. Alle anderen Kandidaten fallen weg. Nach der Bereinigung lässt sich im mittleren Feld der unteren Zeile von Block 8 leicht ein versteckter (Block-)Einer aufspüren: Die 8, als einzige Möglichkeit, einen regulären Platz in Block 8 zu belegen.
Sudoku-Spielplattform/ hidden Subsets (hS)
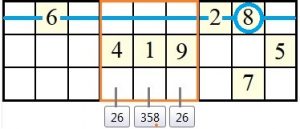
Die soeben am 21er-Sudoku „sudoku_21er.txt“ erläuterte Strategie der hidden Subsets (hS), Feldkandidaten zu reduzieren, lässt sich -in Verbindung mit den Methoden der versteckten und nackten Einer- auf der Sudoku-Spielplattform nachspielen und das Sudoku in nunmehr 12 Spielzügen knacken. Wie oben gezeigt kommt bereits im ersten Spielzug die Strategie der hidden Subsets (hS) zum Einsatz:
Spielzug 1
…
Block 8 – hS (26) || B8 #7 (#76): 23568=>26
Block 8 – hS (26) || B8 #9 (#78): 268=>26
=> Block 8 beherbergt einen hidden Subset (hS) (versteckte Teilmenge), nämlich die Ziffern 26. Betroffen sind in Block 8 die Felder #7 und #9 (Felder #76 und #78). Die Kandidatenlisten der beiden Felder werden bereinigt, d. h. es verbleiben die Ziffern 26 (die versteckte Teilmenge beider Kandidatenlisten) stehen. Daraus ergibt sich ein versteckter (Block-)Einer (vE/B) in diesem Block:
Zeile 9/ Spalte 5/ B8 #8 (#77): – vE/B
=> In Zeile 9, Spalte 5, Block 8, Feld #8 dieses Blocks (Feld #77), findet sich mit der Ziffer 8 ein versteckter (Block-)Einer (vE/B). Grund: In den benachbarten Feldern #77 und #79 des gleichen Blocks 8 wurden via hidden Subsets (hS) die Ziffern 8 aus deren Kandidatenlisten eliminiert. In Block 8 kann die Ziffer 8 daher nur noch in diesem Feld stehen.
Weitere Beispiele
Kombiniert man die Strategie der hidden Subsets (hS) mit der lokalen linearen Suche (lS) benötigt man für das 21er-Sudoku „sudoku_21er.txt“ nur noch neun Spielzüge auf der Sudoku-Spielplattform.
Am Ende von Teil 6
Mit bereits zwei erlernten Sudoku-Strategien in der Tasche, um Kandidatenlisten zu reduzieren, bist du inzwischen in der Lage selbst schwere bis sehr schwierige Sudokus zu knacken. Bei der Strategie der hidden Subset (hS) ist allerdings die Kenntnis aller Kandidaten der noch freien Felder unabdingbar.
Zum nächsten Kapitel Teil 7: Sudoku naked Subsets.
Mit einem Klick finanziert