Die Sudoku-Strategie „X-Wing“ reduziert Kandidaten aus Kandidatenlisten von Zeilen und/oder Spalten, so dass weitere Einer hervortreten.
Kapitel überspringen und gleich zur Sudoku-Spielplattform.
Inhalt Teil 8
Im Teil 7: Sudoku naked Subsets wurde eine Sudoku-Strategie vorgestellt, mit der sich in Kombination mit den zuvor erlernten Strategien selbst schwere, sehr schwere und einige ultraschwierige Sudoku lösbar sind. Auf dieser Seite wird eine weitere fortgeschrittene Strategie, Kandidatenlisten zu reduzieren, erläutert.
X-Wing
Bei der Sudoku-Strategie X-Wing findet sich eine Ziffer (ein Kandidat) nur genau zwei Mal in den Kandidatenlisten zweier Zeilen bzw. zweier Spalten. Stimmen Zeilen und Spalten überein, kann diese Ziffer (dieser Kandidat) aus den Kandidatenlisten aller anderen Felder dieser Spalte bzw. Zeile eliminiert werden.
Beispiel/ X-Wing
Betrachten wir dazu die oberen und unteren drei Blöcken des 21er-Sudoku „sudoku_21er.txt“. In Spalte 4 kommt die Ziffer 6 nur noch genau zwei Mal in den Kandidatenlisten der Felder dieser Spalte vor, nämlich in den Zeilen 1 und 9. Gleiches gilt für die Spalte 6. Auch hier kommt die Ziffer 6 nur noch genau zwei Mal in den Kandidatenlisten der Felder dieser Spalte vor, ebenfalls in den Zeilen 1 und 9. Das bedeutet, dass die Ziffer 6 entweder oben links (Zeile 1, Spalte 4) und unten rechts (Zeile 9, Spalte 6), oder aber, dass die Ziffer 6 unten links (Zeile 9, Spalte 4) und oben rechts (Zeile 1, Spalte 6) stehen wird. Die Ziffern stehen sozusagen „über Kreuz („X“) – in jedem Fall aber wird die Ziffer 6 in den Zeilen 1 und 9 stehen, entweder in Spalte 4 oder Spalte 6 (im Bild gezeigt sind nur die Kandidatenlisten der relevanten Felder):
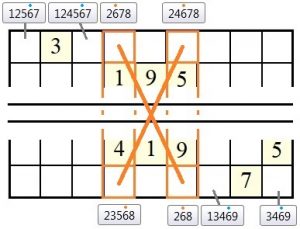
Dadurch, dass die Ziffer 6 in den Spalten 4 oder 6 der Zeilen 1 und 9 stehen wird (man weiß nur noch nicht in welcher Spalte), sind die restlichen Felder der Zeilen 1 und 9 für die Ziffer 6 gesperrt (blaue Linie). Die Ziffer 6 kann also aus den Kandidatenlisten aller anderen Felder dieser Zeilen eliminiert werden. Dies sind in Zeile 1 die Felder #1 und #3 (Spalten 1 und 3), Kandidatenlisten 12567 und 124567, sowie in Zeile 9 die Felder #7 und #9 (Spalten 7 und 9), Kandidatenlisten 13469 und 3469. Damit ergibt sich:
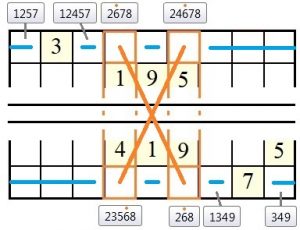
Dadurch lässt sich bspw. in Zeile 6, Spalte 9, ein versteckter (Spalten-)Einer (vE/S) ermitteln (im Bild nicht gezeigt), der von der Sudoku-Spielplattform direkt eingetragen wird.
Sudoku-Spielplattform/ X-Wing
Die soeben am 21er-Sudoku „sudoku_21er.txt“ erläuterte Strategie des X-Wing (xW), Feldkandidaten zu reduzieren, lässt sich -in Verbindung mit den Methoden der versteckten und nackten Einer- auf der Sudoku-Spielplattform nachspielen. Wie oben gezeigt kommt bereits im ersten Spielzug die Strategie des X-Wing (xW) zum Einsatz:
Spielzug 1
…
Z1/9 / S4/6 – xW (6) || Z1 #1 (#1): 12567=>1257
Z1/9 / S4/6 – xW (6) || Z1 #3 (#3): 124567=>12457
Z1/9 / S4/6 – xW (6) || Z9 #7 (#79): 13469=>1349
Z1/9 / S4/6 – xW (6) || Z9 #9 (#81): 3469=>349
=> In den Zeilen 1 und 9 findet sich in den Spalten 4 und 6 ein X-Wing (xW), nämlich die Ziffer 6. Von der Bereinigung betroffen sind in Zeile 1 die Felder #1 und #3 (Spalten 1 und 3) sowie in Zeile 9 die Felder #7 und #9 (Felder #79 und #81, Spalten 7 und 9) – dabei wird jeweils die Ziffer 6 aus den entsprechenden Kandidatenlisten eliminiert.
Durch die Bereinigung der Kandidatenliste in Spalte 9 (Feld #81: 3469=>349) lässt sich für die Ziffer 6 ein versteckter (Spalten-)Einer in Spalte 9 aufspüren:
Zeile 6/ Spalte 9/ B6 #9 (#54): 6 – vE/S
=> In Zeile 6, Spalte 9, Block 6, Feld #9 dieses Blocks (Feld #54) findet sich mit der Ziffer 6 ein versteckter (Spalten-)Einer (vE/S).
Hinweis/ X-Wing
Im oben gezeigten Beispiel findet sich jeweils dieselbe Ziffer nur genau zwei Mal in den Kandidatenlisten zweier Spalten. Daher können Kandidaten aus den betreffenden Zeilen eliminiert werden. Es geht aber auch umgekehrt: eine Ziffer findet sich nur genau zwei Mal in den Kandidatenlisten zweier Zeilen. Dann können Kandidaten aus den betreffenden Spalten eliminiert werden.
Weitere Beispiele
Kombiniert man von Anfang an die Strategie der lokalen linearen Suche (lS), der hidden Subsets (hS), der naked Subsets (nS) und des X-Wing (xW) benötigt man für das sehr schwierige Sudoku „sudoku_4_sehr_schwierig.txt“ auf der Sudoku-Spielplattform sieben Spielzüge.
Am Ende von Teil 8
Mit den bisherigen vier Sudoku-Strategien Kandidatenlisten zu reduzieren, knackst du inzwischen sehr schwierige sowie auch einige ultimativ schwierige Sudokus. Natürlich aber noch längst nicht alle! Hierfür gilt es weitere Strategien zu erlernen – eine weitere findest Du im folgenden Kapitel.
Zum nächsten Kapitel Teil 9: Sudoku Block/Block Interactions.
Mit einem Klick finanziert