Die Sudoku-Strategie „Block/Block Interactions“ reduziert Kandidaten aus Kandidatenlisten von Zeilen und/oder Spalten, so dass weitere Einer hervortreten.
Kapitel überspringen und gleich zur Sudoku-Spielplattform.
Inhalt Teil 9
Im Teil 8: Sudoku X-Wing wurde eine letzte Sudoku-Strategie vorgestellt, mit der sich in Kombination mit den zuvor erlernten Strategien selbst schwere, sehr schwere und einige ultraschwierige Sudoku lösbar sind. Auf dieser Seite wird eine weitere dieser Strategien erklärt.
Block/Block Interactions
Bei der Strategie der Block/Block Interactions sucht man innerhalb zweier Blöcke einer Zeile oder Spalte nach Kandidaten (Ziffern), die nur in zwei Zeilen oder zwei Spalten beider Blöcke vorkommen. Ist dies der Fall, sind beide Zeilen oder Spalten durch diese Ziffer gesperrt, auch wenn man noch nicht genau weiß, an welcher Stelle die Ziffer in den jeweiligen Blöcken steht. Durch die Sperrung kann die Ziffer aber aus den Kandidatenlisten der Felder des dritten Blocks derselben Zeilen oder Spalten eliminiert werden.
Beispiel/ Block/Block Interactions
Betrachten wir dazu die oberen drei Blöcke des Sudoku „sudoku_1_sehr_schwierig_bbI.txt“, bei dem alle bisher bekannten Strategien zunächst erfolglos bleiben. Die Spalten 4 und 9 sind durch die Ziffer 1 gesperrt (orangefarbene Linien). In den Feldern aller anderen Spalten der oberen drei Blöcke kann die Ziffer 1 aber noch stehen. In den Blöcken 1 und 2 sind dies allerdings nur die oberen beiden Zeilen (blau umrandete Felder). D. h. in einem der beiden Blöcke befindet sich die Ziffer 1 in Zeile 1 und im anderen Block in der Zeile 2. Die Zeilen 1 und 2 sind demnach für die Ziffer 1 in Block 3 gesperrt (blaue Linien). Aus den Kandidatenlisten der blau hinterlegten Felder kann die Ziffer 1 daher eliminiert werden:
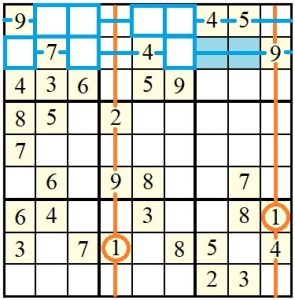
Das gleiche lässt sich auch mit der Ziffer 2 durchführen: Hier sind die Spalten 4 und 7 durch die Ziffer 2 gesperrt (orangefarbene Linien). In den oberen Blöcken 1 und 2 kann die Ziffer 2 wiederum nur in den beiden oberen Zeilen (blau umrandete Felder) stehen. Die Zeilen 1 und 2 sind daher für die Ziffer 2 in Block 3 gesperrt (blaue Linien). Aus den Kandidatenlisten der blau hinterlegten Feldern kann demnach die Ziffer 2 eliminiert werden:
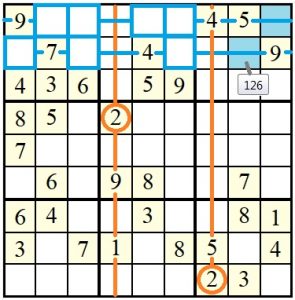
Da in Block 3, Feld #5 dieses Blocks (Feld #17) in Zeile 8, Spalte 8, sowohl die Ziffer 1 als auch die Ziffer 2 eliminiert wurde, bleibt in diesem Feld mit der Ziffer 6 nun ein nackter Einer stehen.
Sudoku Spielplattform/ Block/Block Interactions (bI)
Spielt man das Sudoku „sudoku_1_sehr_schwierig_bbI.txt“ mit der Strategie der Block/Block Interactions (bI) auf der Sudoku-Spielplattform, ergibt sich in der Schritt für Schritt-Lösung:
Spielzug 1
B1/2 / Z1/2 – bI (1) || Z2 #7 (#16): 1368=>368
B1/2 / Z1/2 – bI (1) || Z2 #8 (#17): 126=>26
B1/2 / Z1/2 – bI (2) || Z1 #9 (#9): 23678=>3678
B1/2 / Z1/2 – bI (2) || Z2 #8 (#17): 26=>6
=> In den Blöcken 1 und 2 wurde in den Zeilen 1 und 2 eine Block/Block Interaction (bI) mit der Ziffer 1 ermittelt. Betroffen ist in Zeile 2 das Feld #7 (Feld #16) in Spalte 7, in dem die Ziffer 1 aus der dortigen Kandidatenlisten 1368 eliminiert wird, so dass die Kandidaten 368 übrig bleiben.
=> Ebenfalls betroffen ist in Zeile 2 das Feld #8 (Feld #17) in Spalte 8; hier wird die Ziffer 1 aus der Kandidatenliste 126 eliminiert.
=> In den Blöcken 1 und 2 wurde in den Zeilen 1 und 2 eine Block/Block Interaction (bI) mit der Ziffer 2 ermittelt. Betroffen ist in Zeile 2 das Feld #9, in dem die Ziffer 2 aus der dortigen Kandidatenlisten 23678 eliminiert wird, so dass die Kandidaten 3678 übrig bleiben.
=> Ebenfalls betroffen ist in Zeile 2 das Feld #8 (Feld #17) in Spalte 8; hier wird die Ziffer 2 aus der Kandidatenliste 26 eliminiert.
Im weiteren folgt:
Zeile 2/ Spalte 8/ B3 #5 (#17): 6 – nE
=> Es verbleibt in Zeile 2, Spalte 8, Block 3, Feld #5 dieses Blocks (Feld #17) die Ziffer 6 als nackter Einer (nE) stehen, die in das Spielfeld eingetragen wird.
Hinweis/ Block/Block Interactions (bI)
Block/Block Interactions (bI) sind eine Erweiterung der lokalen linearen Suche (lS). Wird dort nur innerhalb eines Blocks nach Kandidaten gesucht, die in nur einer Zeile oder Spalte auftreten, sucht man hier innerhalb von zwei Blöcken einer Zeile oder Spalte nach Kandidaten, die in genau zwei Zeilen oder Spalten auftreten. Die Suche ist allerdings relativ aufwändig, der Erfolg gering. Bei dem ausgewählten Beispiel-Sudoku ist die Strategie aber erfolgreich, denn dieses lässt sich mit den bisher erlernten Strategien nicht lösen, wie man auf der Sudoku-Spielplattform feststellen kann.
Am Ende von Teil 9
Mit den bisherigen fünf Sudoku-Strategien Kandidatenlisten zu reduzieren, knackst du inzwischen sehr schwierige sowie auch einige ultimativ schwierige Sudokus. Natürlich aber noch längst nicht alle! Hierfür gilt es weitere Strategien zu erlernen, bald, auf dieser Plattform.
Zum nächsten Kapitel Teil 10: Eigene Sudoku spielen.
Mit einem Klick finanziert